神奇測試，馬上知道你的年齡
想隱瞞都不能
一面讀一面做:
[1]首先,挑一個數位(0 -7)表示每個禮拜想出去走走的次數
[2]把這個數位乘上2
[3]然後加上5
[4]再乘以50
[5]如果你今年的生日已經過了，把得到的數目加上1754，
如果還沒過，加1753
[6]最後一個步驟，用這個數目減去你出生的那一年
[7]現在你會有一個三位元數的數位
[8]第一個位數是你一開始選擇的數目(也就是每個星期你希望出去走走的次數)
接下來的二個位數就是你的年齡(要+4)（承認吧）
2009年10月27日 星期二
神奇測試，馬上知道你的年齡，想隱瞞都不能
[補充]循環小數化分數
循環小數化分數
0.75429（429一直無限循環）
429有循環所以要寫成999
75沒循環所以要寫成00
分母就變成99900
而分子就用
『75429－（沒循環的）』
＝75429－75 ＝75354（然後放在分子）
75354/99900
再去給他約分
﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍
例如１：0.45（5一直無限循環）
5有循環所以要寫成9
4沒循環所以要寫成0
分母就變成90
『45－（沒循環的）』
＝45－4
=41（分子）
41/90
例：0.455（55一直無限循環）
55有循環所以要寫成99
4沒循環所以要寫成0
分母就變成990
『455－（沒循環的）』
＝455－4＝451(分子)
＝41/90
[課外補充]費氏數列
[課外補充]費氏數列
蜜蜂與數學
蔡聰明
雄蜂是由未受精的卵孵化出來的，故只有母親而沒有父親。進一步，我們考慮雄蜂的譜系，如圖六，我們發現一隻雄蜂歷代祖先的個數，形成一個費氏數列 (Fibonacci sequence)：
即由首兩項 1, 1 出發，任何一個後項都是前兩項之和。更有趣的是，若各代祖先適當排列的話，第七代的13位祖先恰好可以排成鋼琴八度音之間的13個半音階（8個白鍵，5個黑鍵）。
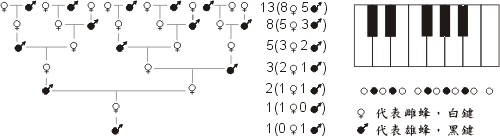 圖六 |
除了雄蜂譜系之外，費氏數學在植物世界偶爾也可以觀察到。有些花草或樹木，其枝幹的分枝成長符合費氏數列的模式，如圖七所示。
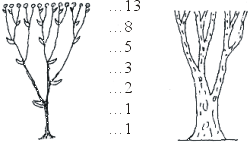 圖七 |
你以後到野外郊遊或登山時，可以留意觀察或找尋看看有沒有符合費氏數列的樹木。筆者曾在登七星山的途中，發現一棵非常「費氏數列」的樹木。懷著一個問題或目標走入大自然，我們才能真正觀察到東西，生活也會更積極主動。
事實上，費氏數列最先是考慮兔子的繁殖引起的。中世紀歐洲最偉大的數學家 Fibonacci（1180～1250）在1202年出版《算盤之書》(Liber Abaci)，其中有一個問題如下：
假設任何一對新出生的兔子，兩個月後開始生一對新兔，以後每隔一個月都生一對新兔。已知年初有一對新兔，在不發生死亡的情況下，問年底總共有幾對兔子？
假設第 n 個月底兔子總共有 an 對，則按題意知
 | (2) |
並且
| an+2=an+1+an | (3) |
(3)式是一個二階差分方程式，(2)式是初期條件。求解(2)與(3)就是要找出通項 an 的公式，這有種種辦法。最早是在1718年由 De Moivre 求得，後來在1843年又由 Binet 重新發現（兩位都是法國數學家），答案是
![\begin{displaymath}<br />a_n=\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^n-(\frac{1-\sqrt{5}}{2})^n]<br />\end{displaymath}](http://episte.math.ntu.edu.tw/articles/sm/sm_27_07_2/img10.gif){kind=small} | (4) |
此式今日叫做 Binet 公式，它含有兩個驚奇：其一是涉及黃金分割的比值 
，其二是整數數列 (an) 居然可用一些無理數的組合來表達。上述兔子問題的答案是 a12=144
蜈蚣穿鞋.....國三機率
蜈蚣穿鞋.....國三機率
有一隻蜈蚣有100隻腳左右邊各50隻腳
有一天他要出去玩
所以要先穿襪再穿鞋子.(一定..不能先穿鞋子再穿襪).襪子沒左右腳之分.鞋子有左右腳之分.請問有多少種解法????(鞋子跟襪子可分開穿
)我的意思是可先穿左1襪...再穿右1襪..再穿左1鞋..
智力測驗三題
智力測驗三題
文章引用http://tw.group.knowledge.yahoo.com/hk09536-84253e/article/view?aid=19
硬幣遊戲
有A、B、C三人，手中各有硬幣若干枚。
開始，A按照B、C兩人手中硬幣數將自己手中的硬幣分別給了他們(比如,B有1枚,就分給他1枚,C有3枚就分給他3枚)，
之後B又按照A、C兩人手中現有的硬幣數將自己手中的硬幣分別給了他們,
最後，C又按A、B兩人手中現有的硬幣數將自己手中的硬幣數分別給了他們。
這樣一來，三人手中硬幣數恰好相等且都是8枚，問他們原來手中硬幣各有幾枚？
解答:
最初A+B+C=24
分到最後
4(A-B-C)=8
2(3B-A-C)=8
7C-A-B=8
所以A=13,B=7,C=4(選取便可看答案)
三人住店
有三個人去住旅館，住三間房，每一間房$10元，於是他們一共付給老闆$30，第二天，老闆覺得三間房只需要$25元就夠了於是叫小弟退回$5給三位客人，誰知小弟貪心只退回每人$1，自己偷偷拿了$2，這樣一來便等於那三位客人每人各花了$9，於是三個人一共花了$27，再加上小弟獨吞了不$2，總共是$29。可是當初他們三個人一共付出$30那?還有$1呢？
解答:
其實這是一個引導你邏輯錯誤的題目，以數學的列式應該是
$30(房客租金) - $3(房客租金退費) = $25(老闆收的租金) + $2(小弟污走的租金)
or
$30(房客租金) - $3(房客租金退費) - $2(小弟污走的租金) = $25(老闆收的租金)
or
$30(房客租金) = $25(老闆收的租金) + $3(房客租金退費) + $2(小弟污走的租金)
小弟污走的租金是從房客租金中扣除的，而非兩者相加(選取便可看答案)
計程車費用
4個人一起去搭計程車,假設計程車的費用與路程成正比
計程車走了1公里後,第一個人下車
再走1公里後,第二個人下車
再走1公里後,第三個人下車
再走1公里後,最後一個人下車並買單
計程車資共花了240元
這4個人應該負擔多少計程車費用才公平呢?
解答:
很多人會回答24,48,72,96元
最公平得分法應該是15,35,65,125元
首先將計程車費240元用分成4份每公里60元
第一公里4人分擔每因此得到15元,15+20=35元,15+20+30=65元,15+20+30+60=125元
人15元
第二公里3人分擔每人20元
第三公里2人分擔每人30元
第四公里1人分擔每人60元(選取便可看到答案)
印度的九九乘法–〔超實用的〕
印度的九九乘法表
是從1 背到19(→19×19乘法？ )，
不過您知道印度人是怎麼記 11到19 的數字嗎？
我是看了下面這本書之後才恍然大悟的。
「印度式計算訓練」
2007年 6月 1 0日第一版第 6刷發行株式會社晉遊社 發售
介紹了加減乘除的各種快速計算方法，
不過在這裡我只介紹印度的九九乘法。因為實在太神奇了！！
下面的數字跟說明都是引用該書P.44 的例子。
請試著用心算算出下面的答案：
13 X 12 = ？
(被乘數) (乘數 )
印度人是這樣算的。
***********************************************************
第一步：
先把被乘數(13)跟乘數的個位數 (2)加起來
13 + 2 = 15
第二步：
! ; ! 然後把第一步的答案乘以10(→也就是說後面加個 0 )
第三步：
再把被乘數的個位數(3)乘以乘數的個位數 (2)
2 X 3 = 6
(13+2)x10 + 6 = 156
**********************************************************
*
就這樣，用心算就可以很快地算出11X11 到19X19了喔。
這真是太神奇了！
我們試著演算一下
14×13：
(1)14+3＝17
(2)17×10＝170
(3)4×3＝12
(4)170+12＝182
16×17：
(1)16+7＝23
(2)23×10＝230
(3)6×7＝42
(4)230+42＝272
真的是耶，好簡單喔
怎不早點讓我知道呢
蠻有知識性的耶 
數學好好玩
數學好好玩
文章引用http://tw.group.knowledge.yahoo.com/andy000-99956/article/view?aid=12
Nice one:
111,111,111 x 111,111,111 = 12,345,678,987,654,321
Trapeze:
3 x 37 = 111
6 x 37 = 222
9 x 37 = 333
12 x 37 = 444
15 x 37 = 555
18 x 37 = 666
21 x 37 = 777
24 x 37 = 888
27 x 37 = 999
0x 9 + 1 = 1
1 x 9 + 2 = 11
12 x 9 + 3 = 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
12345 x 9 + 6 = 111111
123456 x 9 + 7 = 1111111
1234567 x 9 + 8 = 11111111
12345678 x 9 + 9 = 111111111
123456789 x 9+10 = 1111111111
another Trapeze:
1 x 8 + 1 = 9
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 987654321
and another one:
0x 9 + 8 = 8
9 x 9 + 7 = 88
98 x 9 + 6 = 888
987 x 9 + 5 = 8888
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
98765432 x 9 + 0 = 888888888
987654321 x 9 - 1 = 8888888888
9876543210 x 9 - 2 = 88888888888
願大家都 發 發 發發
我在多加一個 是本人【世紀之王】發現的 = =
12345679 x9=111111111
12345679 x18=222222222 12345679 x27=333333333 12345679 x36=444444444 12345679 x45=555555555 12345679 x54=666666666 12345679 x63=777777777 12345679 x72=888888888 12345679 x81=999999999
訂閱：
文章 (Atom)
